what percentage of the area under the normal curve lies as given below? (a) to the right of μ

Math 3118, section 4
Spring 2001
Some facts near the normal curve

Purpose: A bit of further explanation about the normal curve and how to work with it.

As explained in the text, the normal curve is given past the following equation:

We don't have to work directly with this function very often, and so we'll merely need to know almost a few of its basic properties By i of the form exercises, 11.4.2:

• the values of the office are all  > 0.
• the graph of this office is symmetric about the y-axis;
  thus f(ten) = f(-x) for all 10.
• the value of f(10) becomes very small when 10 grows very large.

The graph of the office is shown in Effigy 1 below.

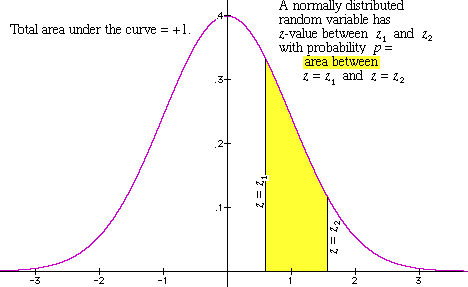
Figure 1: the normal curve

Past definition, a random variable is normally distributed if its probability distribution looks similar the normal curve, suitably shifted and re-scaled. Thus:

• the curve is shifted so that its midpoint corresponds to the mean of our random variable,
• it is stretched and so that 1 unit of measurement of distance from the standard normal bend corresponds to the standard divergence of our random variable, and
• the vertical scale is adjusted so that the full expanse remains equal to 1.
  

We don't take to work directly with the equation here!! Instead, we just have apply Table 11.half-dozen in affiliate xi of the text (on page 254 in the July 17, 2001 version) to find the surface area nether the bend between the two corresponding  z-values. Then, in Figure 1 above, the expanse of the yellow shaded region has to be A(z ₂) -A(z _ane).  This surface area (existence a number between  0  and  1)  tells us the percentage of our probability distribution -- or population -- for which the value of the random variable is inside the indicated range. We'll explain below how to do this in some ofttimes encountered cases.

A couple of instances. In §11.5, nosotros'll run into that the outcome of an independent trials procedure -- repeated a large number of times -- is approximately ordinarily distributed. IQ scores provide another example, as shown in figure 2 below.

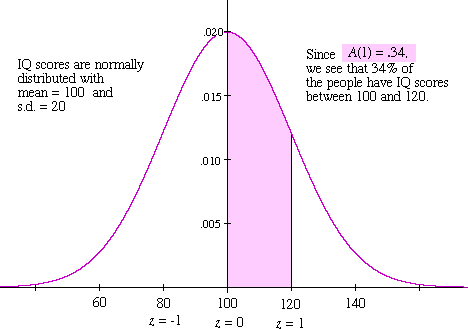
Figure 2: the distribution of IQ scores

This example illustrates the fact that the re-scaling is "nearly invisible". Namely, standard difference is 20, so the divergence between 120 and the hateful ( = 100) is exactly  1  standard deviation unit of measurement. Therefore the area -- shaded in magenta in Figure 2 -- between the corresponding  z-values  (z = 0  and z = one)  is  A(1) = 0.34.  Hence, 34% of the population has IQ scores in this range.

Working with normal distributions

Function I:Determining the per centum of the population when a range of scores is given

1. Finding the expanse to the right of a given [positive] z-value. For example, this is the situation if we're given some examination score above the mean and we want to find what percentage of the people taking the exam had scores above that level.

     For a specific numerical instance, suppose that in a examination with a hateful of 73 and a standard deviation of 6, nosotros want to know how what per centum of the students had scores of 80 or above. (This is like the discussion at the lesser of page 253 or the text.) And so at that place are 3 steps:

   1. Find the  z-value. We piece of work with 79.5 instead of 80; subtract the hateful from this value, and so divide by the standard difference:
      z = = = 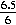1.083.
      
   2. Look up the value of  A(z)  in the table. We circular off to z = 1.1  and and so look up:
      A(1.1) = 0.3643.
      This gives the area that's shaded with ruby stripes in the diagram.
      
   3. Decrease from  0.5  to detect the area of the right-hand tail of the distribution. Thus:
      0.5 - A(one.ane) = 0.5 - 0.3643 = 0.1357.
      This area is shaded with green in the diagram.
   
   Thus, about 13.6%   of the students take scores of 80 or above.
   
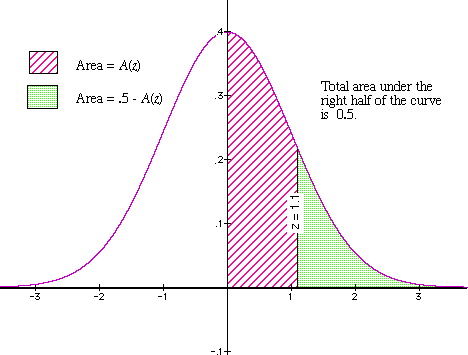
   Effigy 3: A(z) and the area of the "tail"
   
2. Finding the expanse inside a given altitude of the hateful. Given our data virtually IQ scores, suppose we want to know what percentage of the people take IQ score betwixt 75 and 125, inclusive. Assuming that our scores but take integer values, we work with 125.5 and 74.5 when finding the corresponding  z-values.
   1. For a score of 125.five, nosotros obtain:
      z =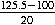 = = 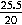one.275.

        For a score of 76.5, a like calculation gives z = -1.275.

   2. Working with the positive value, we circular off to z = one.iii   and look in the table to notice:
      A(1.3) = 0.4032.
      This gives the surface area that's shaded with green stripes in Figure 4.
      
   3. By the symmetry of the graph, the area on the other side (with orange stripes) also has area = 0.4032. [Notation that the z-value on the other side is exactly the negative of the one that we merely looked at.] So, the total shaded area is:
      0.4032 + 0.4032 = 0.8064.
   
   Thus, nearly lxxx.6% of the people take IQ scores between 75 and 125, inclusive.
   
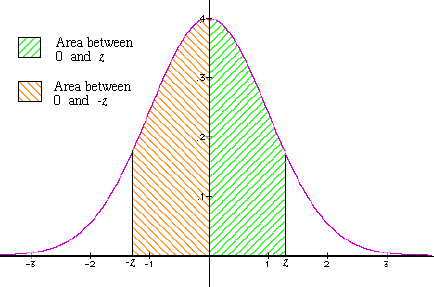
   Figure four: The region within a given distance of the mean
   
3. Finding the expanse to the left of a given [positive] z-value.   Once again, we'll illustrate this with a specific example. So, permit's suppose that k students have taken an exam, where 100 points is the maximum score, the mean is 73, and the standard deviation is 5. We'll ask how many students had scores of 80 or lower.
   1. To find the z-value, we work with 80.5, since this "splits the difference" betwixt eighty and 81. Here is our calculation:
      z =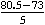 = = 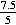1.5.
      
   2. Equally usual, we look in Tabular array eleven.6 to find  A(z):
      A(i.5) = 0.4332.
      This gives the area that's shaded with green stripes in Figure v, respective to scores which are
      higher up the mean but below the indicated z-value.
      
   3. To find the total shaded expanse, we have to add together the surface area to the left of the midpoint -- shaded in turquoise in Figure v. Since it's exactly half of the unabridged area under the normal bend, this area is = 0.5. Hence, the full shaded area is:
               0.five + 0.4332 = .9332.
      
   
   Nosotros conclude that 933 of the 1000 students had test scores of 80 or lower.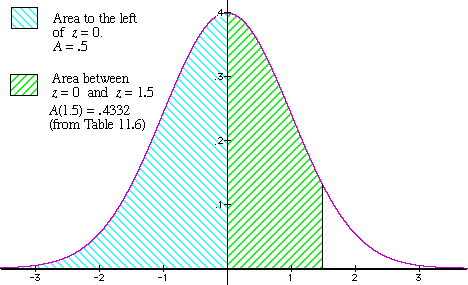
   Figure v: The area to the left of a given positive z-value
   

Part Ii:Determining the range of scores when a percentage of the population is given

Each of these problems is "inverse" to the corresponding problem in Role I. Thus, in Function 1 we were given a range of scores and wanted to discover the percent of the population whose scores are in that range. In terms of Tabular array 11.6, this meant that nosotros calculated z and and so looked upward  A(z).  Hither; the situation is turned effectually. We're given a percentage of the population, and we want to detect what range of scores corresponds to it. And so, we start by figuring out a value for  A(z)  and so looking in the table to find the value of z which corresponds most closely to it.

1. Finding the [positive] z-value such that a given percentage of the area under the normal curve lies to the right of that value.   (This question makes sense merely if the given percentage is< 50%.)

     This is inverse to the trouble discussed in Part IA, so that you can refer to the aforementioned figure. In Part IA nosotros were given the z-value, so we looked up the value of A(z) and then subtracted it from 0.5 to go the expanse of the tail -- shown with the calorie-free green [solid] shading in the effigy. Here, nosotros are given the area of the tail, and then nosotros do the steps in the contrary order, namely:

   1. Subtract from 0.5 to go the surface area under the normal bend between the midpoint (z = 0) and the horizontal line respective to the [nonetheless unknown] z-value. This number is the value of  A(z)  that we have to work with.
   2. We at present "read the table backwards" to find the sought-for z-value. Thus, we await in the right-hand column of Table eleven.half-dozen to find the number that's closest to the value of  A(z)  that we merely calculated. Our z-value is on the aforementioned line in the left-paw cavalcade of the table. For better accurateness, if our value of  A(z)  is about halfway between two entries in the correct manus column of tabular array 11.6, and so we can split up the difference between the 2 corresponding z-values.

        An instance: Allow'south decide the z-value such that 10% of the population has scores above that value. This means that nosotros take to take  A(z) =.five -.1 =.four. Looking in the table, the closest value is  A(z) =.4032,  and this corresponds to z = one.iii. In an applied problem, we withal have to re-scale and shift. For instance in the instance of IQ scores, with  hateful = 100  and  due south.d. = twenty,  a z-value of 1.three corresponds to an IQ score which is  i.3·20 = 26  points above the mean, and thus to a score of  100 + 26 = 126.

2. Finding the [positive] z-value such that a given percent of the surface area nether the normal curve lies within z  standard deviation units of the mean.
     This is inverse to the problem discussed in Part IB, and then that you can refer to the same figure. In Role IB we were given the z-value, so we looked upward the value of A(z) then multiplied information technology 2 to go the area under the the middle part of the bell curve -- shown equally the total of the two shaded areas in the figure. Here, we are given the surface area of the symmetric centre role, so that we have to opposite the social club of the steps and appropriately substitute division for multiplication. Thus:
   1. Separate the given symmetric surface area by 2, in order to discover the value of  A(z).
   2. Look for this value in the correct-hand column of Tabular array xi.vi. Our respond is then the z-value on the aforementioned line of the table. For case, suppose that we want to determine the IQ scores that characterize the heart ² /₃ of the population. Then we accept  A(z) =¹ /₃  ( =^two /₃.¹ /₂ ). Looking in the table, the 2 closest values are  0.3159  and  0.3413.  These correspond to z = 0.9  and z = ane.0  respectively. Accordingly, our reply is virtually halfway between and thus corresponds to z = 0.95. The actual range is between 19 points  ( = 0.95·20) beneath the mean and nineteen points above the mean, i.eastward., IQ scores between 81 and 119.
   
   
3. Finding the [positive] z-value such that a given percent of the area under the normal curve lies to the left of that value.   (This question makes sense only if the given percentage is> 50%.)

     Look at the figure in Function IC to assist with agreement this case. We have to subtract 0.5 from our given area in guild to find the value of  A(z)  to work with. For instance, if nosotros want to find the score corresponding to the 85^th percetile, then we have  A(z) = 0.85 - 0.5 = 0.35. (Etc., past analogy with the other cases ... )

Back to the course homepage

spellmanrouresing77.blogspot.com

Source: https://www-users.cse.umn.edu/~rober005/math3118/normcurves.html

Share this post